Taniyama-Shimura conjecture begins the last part of our story. It was raised for the first time by Yutaka Taniyama, in the form of a problem posed to the participants of an international conference on algebraic number theory that took place in Tokyo in 1955, and published in Japanese a year later. 28-year-old Taniyama was in the beginning of his career as a mathematician, and three years later he had committed suicide. Goro Shimura, a close friend of Taniyama, continued to develop the conjecture, in the late fifties and sixties. André Weil, who also participated in that conference, was the first to encourage the hope that the conjecture is true, and brought it to the attention of a greater audience, as an exercise to the readers of a paper he published in 1967. Considering the many fathers of the conjecture, it was known also as Taniyama-Weil conjecture. The conjecture deals with the properties of elliptic curves.

Elliptic curves are not ellipses but Diophantine equations, of the form y²=Ax³+Bx²+Cx+D. The two dimensional graphical representation of these equations look like a hump with an egg on top. The graphical representation of these equations in complex numbers is what mathematicians call a torus and the rest of the word calls a bagel. Diophantine equations of this class appear in Fermat's work. He had shown, for example, that the equation y²=x-x³ has three rational solutions: (0,0), (1,0) and (-1,0).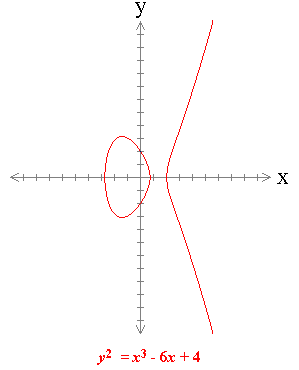

In the twentieth century elliptic curves were an important research topic in number theory, and a lot of knowledge was accumulated about them ("One can write endlessly about elliptic curves" wrote Serge Lang in the preface to his book Elliptic Curves - Diophantine Analysis (published in 1973). In last few years elliptic curves are used in cryptography.

Dealing with elliptic curves was one of the reasons that motivated Mordell to raise his conjecture, although they are not included in the equations dealt by the conjecture as an elliptic curve may have infinite number of solutions. However, Mordell proved that there is a finite group of solutions to an elliptic curve, of them all the solutions may be created using addition and subtraction.

Taniyama-Shimura conjecture became a central problem in number theory, since its proof promised many important results as to the solution of Diophantine equations. As long as there is no proof to Taniyama-Shimura conjecture, all these results rely on moving sands. Like FLT, Taniyama-Shimura conjecture received proofs to many of its special cases, but not the general proof dealing with the infinite set of elliptic curves.

A major breakthrough in the attempts to prove FLT was made in the eighties. Gerhard Frey of Germany assumed that FLT is false, namely that there is a solution that fulfills Aⁿ+Bⁿ=Cⁿ, and checked the properties of the elliptic curve y²=x(x-Aⁿ)(x+Bⁿ) created by this solution. The special properties of this curve, which is part of a set named semi-stable elliptic curves, brought Frey to the conjecture that the curve does not fulfill Taniyama-Shimura conjecture. Frey tried to prove his conjecture, and when he failed to do so, he presented his partial results, in a conference held in the beginning of 1985, hoping to get the help he needed. Jean-Pierre Serre, a French mathematician who was awarded Fields' Medal in 1954, supported Frey's conjecture, by pointing out that Frey's conjecture mesh well with some of his own conjectures. In 1986, Ken Ribet of the University of California at Berkley proved Frey's conjecture (another four years passed till the proof was published).

An immediate result of this proof is that from the proof of Taniyama-Shimura conjecture (if only for semi-stable elliptic curves) the truth of FLT will follow. It created a linkage between FLT and Taniyama-Shimura conjecture, but this linkage is not complete: the refutation of Taniyama-Shimura conjecture says nothing about FLT, and proving FLT says nothing about Taniyama-Shimura conjecture. However, this linkage is enough to turn FLT from an isolated problem into one that is connected to the main research in number theory.

Hilbert's dream was to preserve the unity of mathematics and that mathematics would not split into separate branches, because he viewed mathematics as "an indivisible whole, an organism whose vitality is conditioned upon the connection of its parts". It seems to be that Hilbert is the last one to fulfill this vision. The attempts to prove Taniyama-Shimura conjecture returned to mathematics some of its lost unity. The conjecture itself connects arithmetic and geometry. In an article published in 1991, Barry Mazur of Harvard University pointed out that to prove the conjecture one must step out of the boundaries of number theory and try to find the solution in other branches of mathematics, starting with differential geometry and ending with complex variables.