The news about the linkage created between FLT and Taniyama-Shimura conjecture arrived also to Andrew Wiles, a British mathematician who moved to Princeton University. Wiles spoke of the moment he received the news: "I was electrified. I knew that moment that the course of my life was changing because this meant that to prove Fermat's Last Theorem all I had to do was to prove the Taniyama-Shimura conjecture." And indeed, since that moment, for seven years, Wiles dedicated all his time to find a proof to the Taniyama-Shimura conjecture.

In a conference held in June 1993 in Cambridge University, Wiles gave a series of three lectures named elliptic curves, modular forms and Galois representations. At the end of these lectures he came to a proof of Taniyama-Shimura conjecture for semi-stable elliptic curves. From this proof follows, as Ribet had shown, the proof of Fermat's Last Theorem. The proof, which only its concepts were given in the lectures, was 200 pages long, so it is not surprising that the margins of the book were "too narrow to contain it", as Fermat wrote. The seven years that Wiles devoted to the proof show that the graffiti found in one of the subway tunnels saying: "I have a marvelous proof to Fermat's Last Theorem, but the train is coming already" is far from reflecting the time needed for this proof.

How much excitement can a mathematical proof cause, in the mathematical community and outside it? This was well described by the Israeli writer Amos Oz, in his novel Touch the Water, Touch the Wind, that appeared twenty years before Wiles presented his proof:

"Elisha Pomerantz, a modest, retiring shepherd living in a kibbutz in the north of the country, has unexpectedly published an important article in a leading foreign scientific periodical. The article I by no means modest or insignificant: according to the headlines in the evening newspapers he has succeeded in solving one of the most baffling paradoxes connected with the mathematical concept of infinity.
It was a sensational event. The newspapers even told of a storm of excitement in the most remote centers of learning. Generations upon generations of scholars had broken their heads against the paradoxes of mathematical infinity, had muttered about the limitations of the human mind, had trembled as their thoughts tentatively probed the utmost limits of knowledge and encountered the frosty depths of the universe, adopted a tone of resignation in the face of the silence of eternal mysteries, and had always concluded: thus far and no farther. No one could ever cross their final line without collapsing into contradiction, absurdity, mysticism, ecstasy, or madness. This line marked the final limit of reason and the threshold of silence.
And now, to universal astonishment, a simple amateur, an outsider, working alone in a remote, out-of-the-way village, with the aid of nothing but pencil, paper, and solitude, had probed and hunted and suddenly come up with -
- an astounding theorem.
- a simple solution.
- a crystal-clear answer.
- breathtaking."

Translated from the Hebrew by Nicholas de Lange in collaboration with Amos Oz.

The acceptance of Wiles' proof was far from being typical. Not only the New York Times, known for the large space it leaves to scientific news, broke the news to its readers, but many other newspapers that have never supplied their readers with mathematical news, have done so. Then came a BBC television program, a book that became a bestseller and even an Off Broadway musical named Fermat's Last Tango.

A Czech stamp celebrating the proof of FLT:

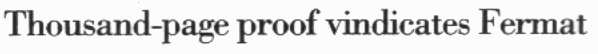Despite the bitter experience with wrong proofs for FLT, mathematicians trusted Wiles' proof before they read the complete proof. That trust was not just because of Wiles' reputation, but also because this proof used a wide range of tools and ideas developed in the last years by mathematicians all over the world. Trust building steps are more common to politicians than to mathematicians, although Fermat was trusted too, as we learn from the name Fermat's Last Theorem: in the past 350 years it should have been called Fermat's Last Conjecture or Fermat's Last Problem, like other unproven conjectures.

Was the trust given to Wiles exaggerated? While reviewing the proof's manuscript for publication in a mathematical journal, some flaws were found and removed. Even without considering the size of the proof, this is not unusual. However, in December 1993, about half a year after presenting his proof, Wiles admitted, in an e-mail sent to his colleagues, that there was a flaw (found by Nick Katz) in the proof and that he believed he can remove it. As time passed without a fix to that flaw, FLT regained its status as an unsolved problem. Remarkable are the words of André Weil: "To some extent, proving Fermat's theorem is like climbing Everest. If a man wants to climb Everest and falls short of it by 100 yards, he has not climbed Everest" . These words also reflect the change in Wiles' working conditions - in the first seven years he worked on FLT under high secrecy, but since he has presented his proof, everyone was watching him trying to remove the flaw.

In November 1994, about a year after the flaw in the proof has been found, Wiles and his former student Richard Taylor reported that they have successfully completed the proof, by replacing its problematic chapter with one that achieves the same goal in a simpler way. The tactic used by Wiles and Taylor was not new to Wiles - he made a similar attempt some years earlier, but abandoned this way in favor of the way found to be finally wrong. The results of their work, which are a proof to Fermat's Last Theorem, were published in two articles in the May 1995 issue of the journal Annals of Mathematics. The longer article is by Wiles and the other by Wiles and Taylor.

How feels a mathematician who created such a marvelous proof? Wiles described it in an interview to the BBC:

"Perhaps I can best describe my experience of doing mathematics in terms of a journey through a dark unexplored mansion. You enter the first room of the mansion and it's completely dark. You stumble around bumping into the furniture, but gradually you learn where each piece of furniture is. Finally, after six months or so, you find the light switch, you turn it on, and suddenly it's all illuminated. You can see exactly where you were."