מי המשולש המבוקש?

האגדה מספרת שפיתגורס חגג את הוכחת המשפט הקרוי על שמו בהקרבת מאה שוורים. אלא שמהר מאוד התבררה תוצאה שהעכירה את השמחה. במשולש ישר זוית שבו אורך כל אחד משני הניצבים הוא 1, אורך היתר הוא , שהוא מספר אירציונלי. פיתגורס, שהאמין כי "הכל מספר", כלומר שהכל ניתן לתיאור כיחסים בין מספרים שלמים, ציווה להטביע בנהר את התלמיד שהגיע לתוצאה זו. שוורים ותלמידים, הזהרו ממורים הנוטים למצבי רוח קיצוניים! (פיתגורס ותלמידיו דגלו בצמחונות ובאהבת הידע, כך שסיפור זה, יותר משהוא משקף אמת היסטורית, משקף את הערפול האופף את תולדותיו של פיתגורס).

חיבתו של פיתגורס למספרים שלמים ממשיכה לספרו של דיופנטוס, "אריתמטיקה", שבו נדרשות תשובות במספרים שלמים. קלוד באשה, שפירסם בשנת 1621 תרגום מוער ללטינית של "אריתמטיקה", מסתפק במעט פחות, ושואל על משולש שצלעותיו וגובהו הם מספרים רציונליים. למעשה אין הקלה גדולה בדרישה זו, משום שהכפלת הצלעות והגובה במכנה המשותף שלהם תהפוך את המספרים הרציונליים למספרים שלמים. משולש שגובהו וכל צלעותיו (ולכן גם שטחו) הם מספרים שלמים קרוי משולש הרוני, על-שמו של הרון מאלכסנדריה.

משולשים הרוניים יש רבים, אך המשולש שאותו אנו מחפשים בחידתנו הוא אחד ויחיד: מצא משולש הרוני שגובהו וצלעותיו מהווים סדרה של ארבעה מספרים עוקבים. רמז: הגובה מחלק את הבסיס לשני חלקים שאף הם מספרים שלמים.

הדרך הפשוטה ביותר ליצור משולש הרוני, ובפרט משולש המקיים גם את הרמז שבחידתנו, היא לבנותו משני משולשים ישרי זוית שצלעותיהם הן מספרים שלמים, כלומר משולשים ישרי זוית שצלעותיהם מהוות שלשה פיתגורית. יש לבחור שני משולשים בעלי ניצב באותו אורך, ולהצמיד אותם לאורך הניצב המשותף (שיהיה הגובה של המשולש ההרוני).
מעיון בתחילתה של רשימת השלשות הפיתגוריות נוכל למצוא שלשה המכילה שני מספרים עוקבים: 5, 12, 13. ניקח את השלשה הראשונה ברשימה: 3, 4, 5, נכפיל את איבריה ב-3 ונקבל את השלשה: 9, 12, 15. נצמיד שני משולשים אלה לאורך הניצב שאורכו 12, ונקבל את המשולש ההרוני המבוקש.

איזה משולש גדול יותר

;

לפניך שני משולשים שווי שוקיים. בשניהם אורך השוק 5 ס"מ. במשולש הימני אורך הבסיס 8 ס"מ ובמשולש השמאלי אורך הבסיס 6 ס"מ. שטחו של איזה משולש גדול יותר?

;

יש בחידה מספיק נתונים כדי לחשב את שטח המשולש לפי נוסחת הרון (הנוסחה לחישוב שטח המשולש לפי אורך צלעותיו), או לחשב את הגובה ואחר כך לחשב את השטח לפי הבסיס והגובה, אבל למה להתאמץ? ברגע שנבנה בכל משולש גובה לבסיס, נגלה שחצינו כל משולש לשני משולשים ישרי זוית שאורך צלעותיהם 3, 4, ו-5 ס"מ, ולכן המשולשים הנתונים שווים בשטחם.

עשרים ואחת קוביות

בספר "בביתו במדבר" מספר מאיר שלו על סתת המכין קוביות אבן לאהובתו (עמ' 144) כך מתאר זאת חברו של הסתת:

"את קוביות האבן שמונחות על מדרגות ביתך מכין ומביא לך ידידי אברהם. סתת צעיר ותמים הוא וסבור שכך ישיג את אהבתך".
...
"בוודאי הבחנת," הוסיף באראדה, "בקסם המיוחד הנסוך על הקוביות הללו. ראשית, כולן נוקרו מסלע אחד של אבן מלכי, האבן המלכה, ושנית, אם תטרחי ותמדדי אותן, תגלי שהאלכסון של כל קובייה הוא מקצועה של הקובייה הגדולה ממנה."
...
"היחס הזה הוא מן היחסים שהם עצם מהותו של היופי. כמו היחס שבין גובה מצחה של אשה ואורך ירכיה, כמו היחס שבין הרווח בין עיניה ובין מוטת כנפי זרועותיה. היחס שבין חלקו החשוף וחלקו המכוסה עלווה של גזע הברוש. כך גם היחס הזה, שבין פיאותיהן ואלכסוניהן של האבנים שסיתת לך חברי אברהם."
...
"אחרי שיביא לך את כל האבנים, עשרים ואחת במספר, ואת תציבי אותן זו ליד זו, תגלי סדרה שאינה משמימה כמו הטור החשבוני ואינה מאיימת כמו טור גיאומטרי."

מדבריו של באראדה, המספר, לא לחלוטין ברור, באמרו "אלכסון של קובייה", האם כוונתו לאלכסון של הפאה או לאלכסון הראשי של הקובייה, זה העובר מפינה אחת של הקובייה לפינה הנגדית לה. לפיכך נפתור את החידה ביחס לשתי האפשרויות.

נתחיל באפשרות לפיה במלה "אלכסון" הכוונה לאלכסון של הפאה. אם אורך המקצוע של הקובייה הקטנה ביותר הוא 1, הרי לפי משפט פיתגורס אורך המקצוע של הקובייה הגדולה ממנה הוא . יחס זה נשמר בין מקצועה של כל קובייה ובין מקצועה של הקובייה הגדולה ממנה, ולכן מקצועה של הקובייה הגדולה ביותר גדול פי ²⁰ = 2¹⁰ = 1024 ממקצועה של הקובייה הקטנה ביותר.

באפשרות השנייה, לפיה במלה "אלכסון" הכוונה היא לאלכסון הראשי של הקובייה, החשבון דומה. האלכסון AD הוא היתר במשולש ישר זוית ACD, ולכן לפי משפט פיתגורס אורכו . לפיכך היחס בין מקצועה של כל קובייה ובין מקצועה של הקובייה הגדולה ממנה הוא , ולכן מקצועה של הקובייה הגדולה ביותר גדול פי ²⁰ = 3¹⁰ = 59,049 ממקצועה של הקובייה הקטנה ביותר.

סדרה של קוביות מופיעה בפסל המינימליסטי "מבנה גאומטרי פתוח IV", שיצר בשנת 1990 האמן האמריקאי סול לה-ויט (Sol LeWitt):

ריבועים ריבועים

במלון "דן פנורמה" שבמרומי הכרמל נמצאת מסעדת "פיתגורס", הקרויה כך על שמו של אורח חשוב שהתגורר זמן מה בכרמל כאלפיים וחמש מאות שנה לפני הקמת המלון. וזו השיחה ששמעתי בעת ביקור במסעדה זו:

"האם שמת לב שמספרי החדרים שקיבלנו הם 100 ו-164?"
"כמובן. יש משהו מיוחד במספרים האלה?"
"כן, ההפרש ביניהם הוא 8², ואם נוסיף להם 125 נקבל עוד שני ריבועים: 15² ו-17², כך שתיווצר לנו שלשה פיתגורית".
"יש מספר קטן יותר שאם נוסיפו למספרי חדרינו נקבל שני ריבועים".

אם נצמצם את חיפושינו לתחום המספרים החיוביים בלבד, לא נמצא את המספר המבוקש, אך אם נרחיב את תחום חיפושינו גם למספרים שליליים - במהרה נמצאנו. אם נוסיף למספרי החדרים 64-, נקבל שני ריבועים: 6² ו-10².

בנה שלושה עשר משולשים ישרי זוית

בטקס בת-מצווה קבוצתי שנערך לתלמידות חטיבת הביניים המדעית קישטו את חצר בית הספר 12 תרנים, ומתוך מבט לשנה הבאה היה גובהו של כל תורן 13 מטרים. כעבור שבוע נערך טקס בר-מצווה קבוצתי לבני הכתה המתמטית, והוחלט שאת בית הספר יקשטו 13 משולשים ישרי זוית. תלמידי הכתה האקולוגית הציעו למחזר למטרה זו את התרנים ששימשו בטקס בת-המצווה, ולנסר לשם כך את התרנים לחתיכות שאורכן 3, 4 ו-5 מטרים. איך יש לנסר את התרנים?

היקפו של כל משולש שעלינו להרכיב הוא 12=3+4+5 מטרים, ולכן ההיקף הכולל של 13 המשולשים הוא 156 מטרים. זהו גם האורך הכולל של 12 התרנים שברשותנו, כלומר החיתוך צריך להיעשות ללא שאריות. תורן שאורכו 13 מטרים ניתן לנסר ללא שאריות, לחתיכות שאורכן 3, 4, ו-5 מטרים, רק בצורות הבאות:

חיתוך מסוג א':	13 = 3+3+3+4
חיתוך מסוג ב':	13 = 3+5+5
חיתוך מסוג ג':	13 = 4+4+5

כדי להגשים את מטרתנו עלינו לנסר x מוטות בחיתוך מסוג א', y מוטות בחיתוך מסוג ב', ו-z מוטות בחיתוך מסוג ג', כך שיתקיימו ארבע המשוואות הבאות:

בסך הכל יש לנו 12 מוטות לחיתוך:	x+y+z = 12
עלינו ליצור 13 חתיכות שאורך כל אחת מהן 3 מטרים:	3x+y = 13
עלינו ליצור 13 חתיכות שאורך כל אחת מהן 4 מטרים:	x+2z = 13
עלינו ליצור 13 חתיכות שאורך כל אחת מהן 5 מטרים:	2y+z = 13

פתרון המשוואות מביא לתוצאה: x=3, y=4, z=5 .

האם ייתכן יתר שאורכו הוא מספר זוגי?

שלשה פיתגורית בסיסית היא שלשה פיתגורית שלשלושת איבריה אין גורם משותף. השלשה 3, 4, 5 היא שלשה בסיסית, ואילו השלשה 12, 16, 20 אינה שלשה בסיסית, משום שלשלושת איבריה יש גורם משותף - 4. הנה דוגמה לשלשות פיתגוריות בסיסיות:

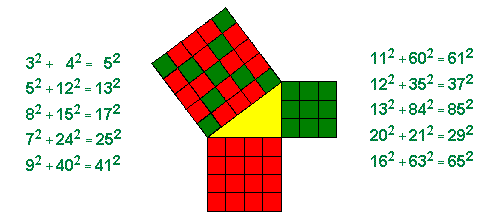
ניכר בדוגמה זו שאורך היתר הוא תמיד מספר אי-זוגי. האם זו תוצאה מקרית, או שבשלשה פיתגורית בסיסית לא ייתכן יתר שאורכו הוא מספר זוגי?

נניח שאורך היתר הוא מספר זוגי, כלומר במשוואה z ,x²+y²=z² הוא מספר זוגי. כתוצאה מכך גם z² הוא מספר זוגי, ולכן עליו להיות סכום של שני מספרים זוגיים או סכום של שני מספרים אי-זוגיים. האפשרות הראשונה נפסלת משום שאם כל אחד משלושת הריבועים הוא מספר זוגי, הרי יש לשלושת מרכיבי השלשה גורם משותף - 2, בניגוד להנחה שזו שלשה פיתגורית בסיסית.

נבחן את האפשרות השנייה, לפיה z² הוא סכום של שני מספרים אי-זוגיים. את המספרים האי-זוגיים ניתן לחלק לשתי קבוצות: אלה שבהתחלקם ב-4 נותנים שארית 1 ואלה שבהתחלקם ב-4 נותנים שארית 3. בין אם מספר אי-זוגי שייך לקבוצה הראשונה ובין אם הוא שייך לקבוצה השנייה, הריבוע שלו שייך לקבוצה הראשונה, כפי שקל לראות מפיתוח הביטוי (4n+1)² והביטוי (4n+3)². לפיכך z², כסכום ריבועים של שני מספרים אי-זוגיים, נותן שארית 2 בהתחלקו ב-4, אך מההנחה ש-z הוא מספר זוגי נובע ש-z² הוא מספר המתחלק ב-4 ללא שארית.

ההנחה שאורך היתר הוא מספר זוגי הובילה אותנו לסתירה, ולכן לא ייתכן שאורך היתר הוא מספר זוגי. תוצאה נוספת מכך היא שבשלשה פיתגורית בסיסית אורכו של אחד הניצבים הוא מספר זוגי, ואורך האחר אי-זוגי.