עקומים אליפטיים אינם אליפסות אלא משוואות דיופנטיות, שלמחלקה פשוטה שלהן הצורה y²=Ax³+Bx²+Cx+D. ייצוגן הגרפי של משוואות אלה הוא בצורה שהמתמטיקאים מכנים טורוס וכל שאר העולם קורא לה כעך. משוואות דיופנטיות אותן ניתן לכלול במחלקה זו מופיעות בעבודתו של פרמה, שהראה, למשל, שלמשוואה y²=x-x³ יש שלושה פתרונות רציונליים: (0,0), (1,0) ו-(1,0-).

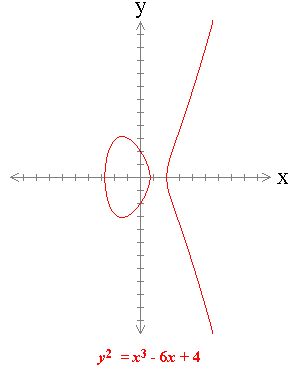במאה העשרים היוו עקומים אליפטיים נושא מחקר חשוב בתורת המספרים, ונצבר אודותם ידע רב ("ניתן לכתוב ללא גבול על עקומים אליפטיים", כתב סרג' לאנג בפתח ספרו "עקומים אליפטיים - אנליזה דיופנטית"). בשנים האחרונות נעשה שימוש בעקומים אליפטיים בקריפטוגרפיה, תורת ההצפנה.

העיסוק בעקומים אליפטיים הוא בין הגורמים שהניעו את מורדל להעלות את השערתו, אם כי אין הם נכללים במשוואות שבהן עוסקת השערת מורדל: לעקום אליפטי ייתכן מספר אינסופי של פתרונות. עם זאת הוכיח מורדל שקיימת קבוצה סופית של פתרונות, מהם אפשר ליצור, באמצעות חיבור וחיסור, את כל הפתרונות.

השערת טניאמה-שימורה הפכה לבעיה מרכזית בתורת המספרים, משום שהוכחתה הבטיחה תוצאות רבות וחשובות בנוגע לפתרונן של משוואות דיופנטיות. כל עוד אין הוכחה להשערת טניאמה-שימורה, נשענות תוצאות אלה על כרעי תרנגולת, גם כאשר להן עצמן ניתנה הוכחה פורמלית. בדומה למשפט פרמה, זכתה גם השערת טניאמה-שימורה להוכחה של מקרים פרטיים רבים שלה, אך לא להוכחה כללית המתייחסת לקבוצה האינסופית של עקומים אליפטיים.

פריצת דרך חשובה בהוכחתו של משפט פרמה נעשתה בשנות השמונים. גרהרד פרי (Frey) מגרמניה יצא מנקודת הנחה שמשפט פרמה אינו נכון, כלומר יש פתרון המקיים Aⁿ+Bⁿ=Cⁿ ובדק את תכונותיו של העקום האליפטי y²=x(x-Aⁿ)(x+Bⁿ) הנוצר באמצעות פתרון זה. תכונותיו המיוחדות של עקום זה, הנכלל במחלקה הקרויה "עקומים אליפטיים יציבים למחצה", הביאו את פרי להשערה שהעקום אינו מקיים את השערת טניאמה-שימורה. פרי ניסה להוכיח את נכונות השערתו, ומשלא עלה הדבר בידו הסתפק בהצגה של התוצאות החלקיות אליהן הגיע, בכנס שנערך בתחילת שנת 1985 . ז'אן-פייר סר, מתמטיקאי צרפתי, תמך בהשערתו של פרי, ובשנת 1986 הוכיח אותה קנת ריבט (Ribet) מאוניברסיטת קליפורניה בברקלי (עוד ארבע שנים חלפו עד שההוכחה הופיעה בדפוס).

מסקנה מיידית מהוכחה זו היא שמהוכחתה של השערת טניאמה-שימורה (ולו רק לגבי עקומים אליפטיים יציבים למחצה) נובעת נכונותו של משפט פרמה. בכך נוצרה זיקה בין משפט פרמה לבין השערת טניאמה-שימורה, אם כי זיקה זו אינה מלאה: הפרכתה של השערת טניאמה-שימורה אינה אומרת דבר אודות משפט פרמה, והוכחתו של משפט פרמה אינה אומרת דבר אודות השערת טניאמה-שימורה. בכל זאת די בזיקה זו כדי להפוך את משפט פרמה מבעיה מבודדת לבעיה הקשורה לטבורו של המחקר בתורת המספרים.

חלומו של הילברט היה שתשמר אחדותה של המתמטיקה, וזו לא תתפצל לענפים נפרדים וזרים, משום שראה במתמטיקה "אורגניזם שעצם חיוניותו מבוססת על הקשר בין חלקיו". כנראה שהילברט הוא האחרון שהצליח להגשים חלום זה. המאמצים להוכחתה של השערת טניאמה-שימורה החזירו למתמטיקה מעט מהאחדות שאבדה לה. כבר ההשערה עצמה קושרת בין האריתמטיקה לגיאומטריה. במאמר שפורסם בשנת 1991 ציין בארי מזור מאוניברסיטת הארוארד שלהוכחת ההשערה יש לצאת מגבולות תורת המספרים, ולנסות לחפש פתרון בענפים אחרים של המתמטיקה, החל בגיאומטריה דיפרנציאלית וכלה במשתנים מרוכבים.