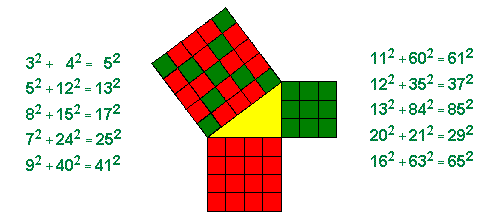
למשוואה x²+y²=z² פתרונות רבים שבהם y ,x ו-z הם מספרים שלמים, למשל: 3²+4²=5² או .5²+12²=13² שלשה כזו קרויה "שלשה פיתגורית", משום שבעקבות משפט פיתגורס היא מתאימה לאורך צלעותיו של משולש ישר זוית. בלוח חימר בבלי, "פלימפטון 322", מלפני כ-3,500 שנה (כאלף שנה לפני זמנו של פיתגורס) נמצאה רשימה של חמש-עשרה שלשות פיתגוריות. סביר להניח, לפי גודל המספרים המופיעים ברשימה, שלמחבר הרשימה היתה שיטה למציאת שלשות פיתגוריות, אך שיטתו אינה ידועה לנו. שיטה ליצירת כל השלשות הפיתגוריות, שמספרן אינסופי, מופיעה בספרו המפורסם של אוקלידס, "יסודות", שנכתב במאה הרביעית לפני הספירה (ועל תוכנו מתבססים לימודי הגיאומטריה בבית הספר התיכון עד עצם היום הזה).

הבעיה של מציאת שלשות פיתגוריות היא דוגמה לסוג של בעיות שבהן עסק דיופנטוס, והקרויות על-שמו "משוואות דיופנטיות". במשוואות אלה מספר הנעלמים גדול ממספר המשוואות, ויש למצוא להן פתרונות במספרים שלמים בלבד. דיופנטוס היה מתמטיקאי יווני בן המאה השלישית, שפעל באלכסנדריה שבמצרים. כמחצית משלושה-עשר הכרכים של "אריתמטיקה", ספרו העיקרי, שרדו עד ימינו (גורל דומה פקד ספרים נוספים של מתמטיקאים יווניים, ויש מהם שהגיעו לידינו רק בתרגומם לערבית).

פירוש ראשון לספרו של דיופנטוס נתחבר בתחילת המאה החמישית על-ידי היפאטיה מאלכסנדריה, אך, ככל כתביה, אבד גם הוא. שני פירושים נוספים נתחברו בסוף המאה השלוש-עשרה על-ידי ביזנטים: התאולוג גאורגיוס פאכימרס (ספר נוסף שלו עוסק בתולדות האימפריה הביזנטית), והנזיר מכסימוס פלאנודס (הידוע יותר באנתולוגיה היוונית שערך). למערב אירופה הגיע הספר באמצע המאה החמש-עשרה, בידי מלומדים ביזנטיים שברחו מקונסטנטינופול עם נפילתה בידי התורכים. רק מאה ושבעים שנה לאחר מכן הפך הספר לנחלת הכלל, כאשר בשנת 1621 פירסם קלוד בשה ספר ובו המקור היווני ובצידו תרגום מוער ללטינית. עותק של ספר זה שימש גם את פרמה.

מעבר מבעיה נתונה לבעיה כללית יותר הוא צעד מקובל ביצירה המתמטית, אם כי מציאת ההכללה הנאותה אינה דבר של מה בכך. בעת שעיין בספרו של דיופנטוס, הירהר פרמה בצורה כללית יותר של המשוואה הפיתגורית, צורה שבה החזקה היא 3, 4 וכו', כלומר (בכתיב מודרני) במשוואה xⁿ+yⁿ=zⁿ. האם למשוואה זו יש פתרון בשלמים גם כאשר n גדול מ-2 ? בשולי הספר כתב פרמה שהתשובה לשאלה זו היא שלילית. כאמור בהערתו המצוטטת לעיל, הוא לא סיפק הוכחה לכך.

פרמה, "נסיך החובבים", חי בטולוז שבדרום צרפת בשנים 1665-1601 (תקופתם של הקרדינלים רישלייה ומאזארן), והיה הפורה במתמטיקאים בדורו. פרמה ידוע בעיקר כאביה של תורת המספרים, שהיא ענף המתמטיקה העוסק ביסודו במספרים שלמים. בנוסף לכך נמנה פרמה עם מניחי היסודות לגיאומטריה האנליטית, החשבון האינפיניטסימלי ותורת ההסתברות. פרמה לא טרח לפרסם את יצירתו, ורק חיבור מתמטי אחד שלו פורסם עוד בחייו. לעומת זאת הרבה פרמה להתכתב עם מתמטיקאים בצרפת וברחבי אירופה, ובהם בלז פסקל, ג'ון ואליס, ובפרט מרן מרסן, שהיה גם ידידו הנאמן של רנה דקארט (וקישר בינו לבין פרמה). חמש שנים לאחר מותו של פרמה, הוציא לאור בנו סמואל את גירסת באשה לספרו של דיופנטוס, בתוספת כל ההערות שכתב פרמה בשולי הספר. את מרבית שאר יצירתו של פרמה, כולל מכתביו שנאספו מחבריו לעט, פירסם הבן כעבור תשע שנים נוספות.

מנהגו של פרמה שלא לרשום הוכחות לטענותיו, דרש עמל רב מבני דורו והדורות הבאים שטרחו להוכיח משפטים אלה. את המשפט שבו אנו עוסקים ניסח פרמה בערך בשנת 1637, והכינוי "אחרון" מציין שזה המשפט האחרון שנותר להוכחה, לאחר שעד תחילת המאה התשע-עשרה ניתנו הוכחות לכל שאר המשפטים שניסח פרמה.

בעיות מתמטיות שפתרונן הצריך מאות שנים שזורות בתולדות המתמטיקה. תורת המספרים גדושה בבעיות כאלה, ולא מעטות מהן מתאפיינות בפשטות ניסוחן. בנוסף למשפט פרמה, זכתה לפרסום גם "השערת גולדבך", האומרת שכל מספר זוגי (גדול מ-2) ניתן להצגה כסכום של שני מספרים ראשוניים. מספר ראשוני הוא מספר המתחלק ללא שארית בשני מספרים בלבד: בעצמו ובאחד. תחילתה של סדרת המספרים הראשוניים היא המספרים ,2 ,3 ,5 ,7 ,11 וכו'. "המשפט היסודי של האריתמטיקה" קובע שלכל מספר שלם קיימת הצגה יחידה כמכפלה של מספרים ראשוניים (למשל: ). תכונה זו של המספרים הראשוניים הופכת אותם למעין "אטומים" של המספרים השלמים.