Not only the long quest to find the mysterious proof of Fermat contributed to the attraction of FLT, but also its simplicity: every high school student can understand it. This property is typical to some other unsolved problems in number theory (like Goldbach's conjecture), and it also motivated people who were not professional mathematicians to try to achieve glory by proving those conjectures. One unconventional way to do it: applying necromancy in order to hear the unwritten proof directly from Fermat's spirit. Some money prizes that were offered for finding a proof for FLT amplified its fame and the enthusiasm to prove it. "The mathematicians do not sleep and do not eat, only banging their heads to the wall while trying to find a complete proof for Fermat's Last Theorem", this vivid description appears in a youth novel, published in 1937, by the Polish author Kornel Makuszynski, Szatan z Siodmej Klasy (The Devil of the Seventh Grade), which one of its heroes is an amateur mathematician, who is devoting many years to fruitless attempts to prove FLT.

In contrast with this enthusiasm, the reluctance of famous mathematicians to tackle this problem is quite remarkable. Gauss dealt with FLT, and after failing to prove it had written: "Fermat's Last Theorem, as an isolated proposition, has very little interest for me, for I could easily lay down a multitude of such propositions, which one could neither prove nor disprove". The German mathematician David Hilbert, the greatest of his time, was asked in 1920 why he was not trying to solve FLT, and answered: "Before beginning I should put in three years of intensive study, and I haven't that much time to squander on a probable failure". I must admit that behind these quotations there are most convincing arguments, not seen at first sight, but there is not enough space in this site to contain them.

The fear of mathematicians of FLT resulted from the experience of their predecessors, but in 1931 the Austrian (and later American) logician, Kurt Gödel, supplied a theoretical foundation to that fear. Till that time, it was assumed with great confidence that when handling any mathematical conjecture there are only two directions: proving the conjecture or refuting it. Hard as it may be to solve a certain problem, a solution does exist. Hilbert knew that this was an unproven belief, but he described it clearly: "The conviction of the solvability of every mathematical problem is a powerful incentive to the worker. We hear within us the perpetual call: There is the problem. Seek its solution. You can find it by pure reason, for in mathematics there is no ignorabimus."

Gödel's incompleteness theorem, which is a cornerstone of mathematical logic, squashed this wonderful belief, by adding a third option to the possible fate of a mathematical conjecture. This theorem states that in any comprehensive logical system, it is possible to state conjectures that are undecidable, namely can neither be proven nor disproven. This is a modern version of the ancient paradox known as the liar paradox, which asks to decide whether the statement "this statement is false" is either true or false. As long as we have no proof of FLT, it may be included in the third category.

Thus, when we have a conjecture, is there a method to identify that this is an undecidable conjecture, so we will not waste our time on it? The British mathematician Alan Turing checked the possibility of building a machine that will accept any conjecture and will determine whether it is a decidable one. To do it, Turing invented a very simple machine, which is equivalent, according to its ability to perform computational tasks, to the most sophisticated computer. Using this virtual "machine" Turing proved, in 1937, that it is impossible to build a machine that give the required answer. Turing machine, which was created within the framework of theoretical research on the foundations of mathematics, was a major contribution to the creation of the electronic computer, and especially to the understanding of its limits.

Under these circumstances, it is possible to understand the note of despair in the words of Harry Vandiver, a mathematician of the University of Texas who devoted his life to the study of FLT. The end of the entry he wrote in the Encyclopedia Britannica on FLT says: "It may be that the theorem will never be proved or disproved".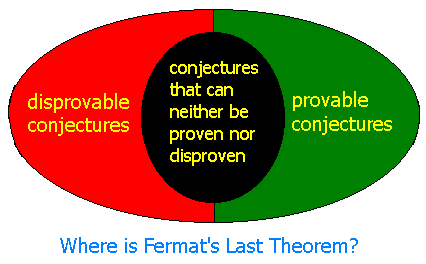

From the dead end that we might arrive at, there is one possible step. Now we do not know to which of the three categories mentioned above FLT belongs. If we prove that FLT belongs to the category of the undecidable conjectures, it will be clear that the theorem is true (although unprovable). The reason of this conclusion is that if the theorem is not true, it means that it has some counterexample. Finding a counterexample, even if it takes a very long time, disproves the theorem, in contradiction to the proof that FLT belongs to the category of the undecidable conjectures.