"I have discovered a marvelous proof to this theorem, that this margin is too narrow to contain", so had scribbled Pierre de Fermat, about 350 years ago, in the margin of a mathematics book he read. That theorem came to be known as Fermat's Last Theorem (which will be abbreviated hence as FLT), and the attempt to prove it had baffled many mathematicians, both professionals and amateurs.

The equation x²+y²=z² has many solutions where x, y, and z are integers, i.e. ,3²+4²=5², or 5²+12²=13². Such a solution is called a Pythagorean triplet, because according to Pythagoras' Theorem such a triplet represents the sides of a right-angled triangle. On a Babylonian clay tablet dated about 3,500 years ago (about 1,000 years preceding Pythagoras) there was found a list of fifteen Pythagorean triplets. It is reasonable to assume, according to the size of the numbers on the list, that its creator had a systematic way of finding Pythagorean triplets, but we do not know his method. A technique to create the infinite list of all Pythagorean triplets appears in Euclid's famous book, the Elements, which was written in the fourth century BC

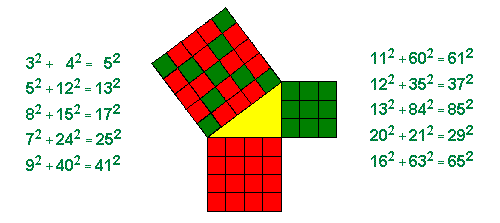The problem of finding Pythagorean triplets is an example to a type of problems that occupied Diophantus, whom after are named "Diophantine equations". In these equations, the number of unknowns is greater than the number of equations, and the required solution must be in integers only. Diophantus was a Greek mathematician of the third century, who lived in Alexandria (Egypt). Only half of the thirteen volumes of his book Arithmetica survived to present day. Many books of Greek mathematicians suffered a similar fate, and some of them survived only through their translation to Arabic.

Hypatia of Alexandria published, in the beginning of the fifth century, a first commentary to Diophantus' book, but it was lost, like the rest of her writings. Two more commentaries were created, in the thirteenth century, by Byzantines: the theologian Georgius Pachymeres (who also wrote a book about the history of the Byzantine Empire) and the monk Maximus Planudes (better known by his Greek anthology). Byzantine scholars, who fled from Constantinople in the middle of the fifteenth century, brought the book to Western Europe. It wasn't for another 170 years that the book became known to the public, when, in 1621, Claude Bachet published a Latin translation of it. A copy of this book was used by Fermat.

Proceeding from a given problem to a more general one is common practice in mathematics, although finding the right generalization is not so simple. While reading Diophantus' book, Fermat thought about a more general version of the Pythagorean equation, where the power is 3, 4 etc., or, in modern notation, the equation xⁿ+yⁿ=zⁿ. Does this equation have a solution in integers when n is greater than 2? In the margin of the book Fermat wrote that the answer is negative, but, as he said in his above-mentioned remark, he did not supply the proof.

Fermat, "prince of amateurs", lived in Toulouse, southern France, in the years 1601-1665 (the period of the cardinals Richelieu and Mazarin), and was the most productive mathematician of that generation. Fermat is known best as father of Number Theory, the branch of mathematics dealing mainly with whole numbers. Fermat was also one of the founders of Analytical Geometry, Calculus and Probability. Fermat did not bother to publish his work, and only one mathematical essay written by him was published in his lifetime. Fermat had a vast correspondence with mathematicians in France and all over Europe, among them Blaise Pascal and his father Etienne Pascal, John Wallis, and especially Marin Mersenne, who was also a friend of René Descartes (and connected between Fermat and Descartes). Five years after Fermat's death, his son, Samuel, published Bachet's version of Diophantus' book, with all the remarks written by Fermat on the margins of the book. Nine years later he published most of the rest of Fermat's writings, including letters collected from his pen pals.

A stamp issued in France in 2001 on the 400th anniversary of Fermat's birth:

Fermat's habit not to give proofs to his theorems demanded much labor from his contemporaries and from mathematicians of the following generations, which tried to prove those theorems. Fermat wrote the theorem at case in about 1637, and the name "Last" means that this is the last of Fermat's theorems that needed a proof, after all others being proved by the beginning of the nineteenth century.

Mathematical problems that required hundreds of years to be proved are part of the history of mathematics. Number theory is packed with such problems, some of them characterized by the simplicity of their wording. Another famous problem is Goldbach's conjecture, which states that each even number (greater than 2) can be represented as a sum of two prime numbers. A prime number is a number divisible by exactly two numbers, itself and 1. The beginning of the series of prime numbers is 2, 3, 5, 7, 11, etc. The fundamental theorem of arithmetic states that each whole number has a single representation as a product of prime numbers (i.e. ). This property of the prime numbers makes them "atoms" of whole numbers.

Fermat left many theorems concerning prime numbers. Using a proof method invented by him, infinite descent, Fermat proved that every prime of the form 4n+1 is the sum of two squares (i.e. 13=2²+3²). Fermat tried to find a formula for creating primes only, but his conjecture as to that formula was found to be wrong. This is the only conjecture made by Fermat that was found to be wrong, and Fermat said he was unable to prove it.